Het gemiddelde van een aantal waarden is gelijk aan de som van die waarden gedeeld door het aantal waarden.

Het populatie gemiddelde is het gemiddelde van alle N waarden in de populatie.
Het steekproef gemiddelde is het gemiddelde van de n waarden in een steekproef.
De mediaan is het midden van een rij geordende getallen. Bij een oneven aantal getallen is de mediaan het middelste getal. Bij een even aantal getallen is de mediaan het gemiddelde van de twee middelste getallen.
Een kwartiel is een vierde deel van een geordende rij gegevens.
Het eerste kwartiel (Q1) is een zodanige maat dat 25% van alle waarden in een verzameling gegevens kleiner is dan deze maat.
Het tweede kwartiel (Q2) is de mediaan, oftewel een zodanige maat dat 50% van alle waarden in een verzameling gegevens kleiner is dan deze maat.
Het derde kwartiel (Q3) is een zodanige maat dat 75% van alle waarden in een verzameling gegevens kleiner is dan deze maat.
De modus is de meest voorkomende waarde.
Module 3,
Het centrum en de spreiding
Wat doe je als je een lading gegevens op je bord krijgt? Het is niet verstandig om als een gek te beginnen met analyseren. Je kan beter eerst overzicht proberen te krijgen. Dit kun je krijgen door een aantal samenvattende maten te berekenen. Allereerst zijn er de maten die het centrum of het midden aangeven. Dan zijn er maten die de variabiliteit in gegevens weergeven. Als laatste heb je nog maten voor relaties tussen verschillende gegevens. Al deze typen maten zal ik in Module 3 bespreken. Ik ga er daarbij van uit dat je bekend bent met basisbegrippen uit Module 1 zoals steekproef, populatie, variabele en parameter. Ook ga ik er van uit dat je vertrouwd genoeg bent met het maken, lezen en interpreteren van tabellen en grafieken, zoals in Module 2.
les 3.1 Centrummaten
Als eerste van alle samenvattende maten is er de centrummaat. Wat is een centrummaat?
Dit is een maat, het woord zegt het al, voor de centrale ligging, oftewel het centrum, van gegevens. Kijk eens naar onderstaande getallenbrei. Wat denk je, is 94 het centrum van alle gegevens?
21 58 44 30 95 48 16
15 7 7819 82 45 20
55 82 18 94 9763 64
47 31 13 58 99 84
5347 59 57 33 84
Ja, in een bepaald opzicht. Het getal 94 ligt in het midden van alle hier gepresenteerde getallen. Echter, als je de getallen wat husselt ligt een ander getal in het midden, terwijl er helemaal niets aan de waarden van deze getallen verandert is. Bij een statistische centrummaat gaat het juist om het centrum van de waarden. Om een idee te krijgen wat een centrummaat is, kan je er het beste een paar bekijken.
Het gemiddelde
De bekendste (statistische) centrummaat is het gemiddelde. Het gemiddelde krijg je door alle waarden in een verzameling gegevens op te tellen en te delen door het aantal waarden.
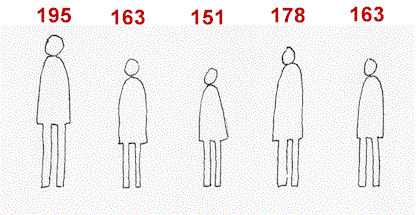
Zo is de gemiddelde lengte van deze vijf mensen het totaal van 195 + 163 + 151 + 178 + 163 = 850 gedeeld door het aantal mensen, dat is 5. Deze vijf zijn dus gemiddeld
![]()
Als je geen 5 maar N waarden hebt, van x1 tot en met xN, dan is het gemiddelde te berekenen door:
![]()
De puntjes in deze formule staan er omdat het wat veel wordt om alle waarden tussen x2 en xN, dat zijn dus x3 tot en met xN-1 ,te noteren. De formule voor het gemiddelde kan echter nog korter. Dit doe je door gebruik te maken van de Griekse letter (spreek uit: “sigma”). Dit symbool wordt algemeen gebruikt als sommatie teken. De formule voor de berekening van het gemiddelde komt er dan zo uit te zien:
![]()
In woorden staat hier: sommeer alle waarden xi van i = 1 tot en met N, en deel vervolgens door N. In het voorbeeld van de lengtes van de vijf mensen geldt dus voor het gemiddelde:
Een gemiddelde dat gebaseerd is op alle N waarden in een populatie is een populatiegemiddelde. Deze wordt weergegeven door de Griekse letter m (spreek uit: “mu”):
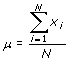
Een gemiddelde dat gebaseerd is op de n waarden in een steekproef is een steekproefgemiddelde. Deze wordt ter onderscheid met het populatiegemiddelde weergegeven door :
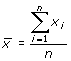
Van hoeveel getallen (n) wil je het gemiddelde bepalen?
De mediaan
Een tweede centrummaat is de mediaan. Dit is letterlijk het midden van een rij getallen, maar dan wel nadat de waarden in volgorde van laag naar hoog zijn geordend.
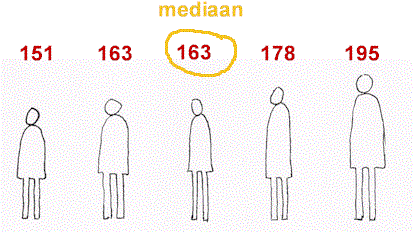
Bij een even aantal getallen is er niet één midden, maar zijn er twee. Het gemiddelde van deze twee is de mediaan.
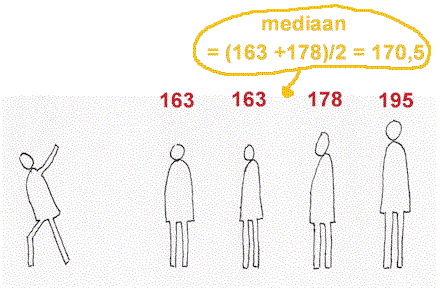
Voor een reeks getallen geldt dus dat 50% van de overige waarden onder de mediaan ligt en 50% erboven. Er zijn natuurlijk ook maten te verzinnen waaronder 40% van de waarden ligt, of 30% of 10%. De maat waaronder 25% van alle waarden in een reeks ligt wordt het eerste kwartiel (Q1) genoemd. Dit is het midden van alle waarden in de reeks die kleiner zijn dan de mediaan. De waarde waaronder 75% van alle waarden in een reeks ligt wordt derde kwartiel (Q3) genoemd. Dit is het midden van alle waarden hoger dan de mediaan. In overeenstemming hiermee wordt de mediaan zelf ook wel het tweede kwartiel (Q2) genoemd. De drie kwartielen delen de gegevens in 4 gelijke groepen. Bij de onderstaande reeks zijn Q1, Q2 en Q3 respectievelijk 2,5 en 8.
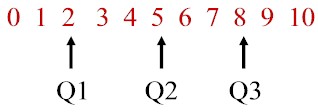
De modus
De laatste centrummaat die ik wil noemen is de modus. Dit is de waarde die het meest voorkomt. Onder de lengtes van de 5 mensen komt 163 cm twee maal voor, terwijl de andere waarden slechts één keer voorkomen. Dus is 163 de modus.
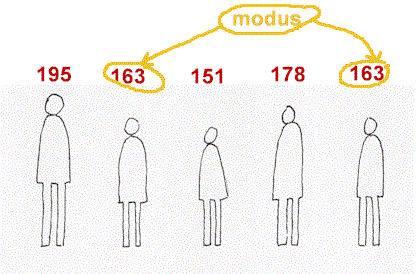
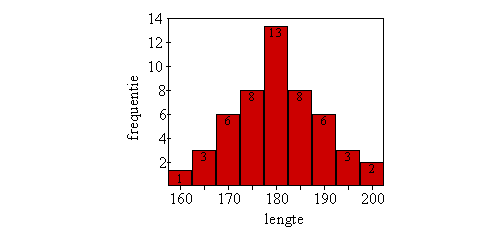
Bij zo weinig getallen als in dit voorbeeld is de modus vrij nietszeggend. Deze wordt pas belangrijk bij een groot aantal waarden, met name als deze in klassen zijn ingedeeld zoals bij een histogram.
In module 2 maakte je kennis met Eva die een T-shirt voor studenten heeft ontworpen. Om een idee te krijgen hoe lang studenten zijn vroeg ze naar de lengte van 50 mannelijke studenten en 50 vrouwelijke studenten. Hieronder is Eva’s histogram van de lengtes van de 50 mannelijke studenten nogmaals weergegeven. Je kunt zien dat lengtes rond de 180 cm het meest voorkomen bij deze studenten. De top van het histogram ligt boven het klassenmidden van 180 cm. Dit is de modus van het histogram.