De Hypergeometrische verdeling

De Hypergeometrische verdeling

De hypergeometrische verdeling wordt gebruikt in een situatie waarbij er in principe twee mogelijkheden zijn: succes of geen succes. Het aantal successen in de eindige niet al te grote populatie (ter grootte van N) is bekend en gelijk aan M. De hypergeometrische verdeling geeft voor een steekproef ter grootte van n die zonder terugleggen wordt getrokken de kans deze x successen bevat. Deze kans wordt als volgt berekent:

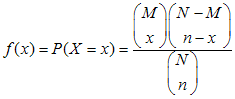
Hieronder alleen een voorbeeld tabel voor N = 100, met M = 5, 10, 20, 50, 80, 90 en 95 en n = 5, 10, 20 en 25 en alle daarbij mogelijke successen. Er zijn nog ontelbaar veel andere tabellen mogelijk, maar helaas is het onmogelijk om deze allemaal hier weer te geven. Voor het berekenen van kansen in situaties waarvoor hier geen tabel is verwijs ik naar tabellen in de statistische literatuur en computerprogramma’s (zoals klik hier). Of probeer zelf de formule in te vullen en uit te rekenen.

n = 5

x	M
x	10	20	30	50	80	90	95	99
0	0,5838	0,3193	0,1608	0,0281	0,0002	0,0000	0,0000	-
1	0,3394	0,4201	0,3654	0,1529	0,0051	0,0002	0,0000	-
2	0,0702	0,2073	0,3162	0,3189	0,0478	0,0064	0,0006	-
3	0,0064	0,0478	0,1302	0,3189	0,2073	0,0702	0,0184	-
4	0,0003	0,0051	0,0255	0,1529	0,4201	0,3393	0,2114	0,05
5	0,0000	0,0002	0,0002	0,0281	0,3193	0,5837	0,7696	0,95

n = 10

x	M
x	10	20	20	50	80	90	95	99
0	0,3305	0,0951	0,0229	0,0006	0,0000	0,0000	-	-
1	0,4080	0,2680	0,1127	0,0072	0,0000	0,0000	-	-
2	0,2015	0,3182	0,2372	0,0380	0,0000	0,0000	-	-
3	0,0518	0,2092	0,2811	0,1131	0,0004	0,0000	-	-
4	0,0076	0,0841	0,2076	0,2114	0,0035	0,0000	-	-
5	0,0006	0,0215	0,0996	0,2593	0,0215	0,0006	0,0000	-
6	0,0000	0,0035	0,0315	0,2114	0,0841	0,0076	0,0003	-
7	0,0000	0,0004	0,0064	0,1131	0,2092	0,0520	0,0064	-
8	0,0000	0,0000	0,0008	0,0380	0,3182	0,2015	0,0702	-
9	0,0000	0,0000	0,0000	0,0072	0,2679	0,4080	0,3394	0,1
10	0,0000	0,0000	0,0000	0,0000	0,0951	0,3304	0,05838	0,9
n = 20

x	M
x	10	20	30	50	80	90	95	99
0	0,0951	0,0066	0,0003	0,0000	0,0000	-	-	-
1	0,2679	0,0433	0,0036	0,0000	0,0000	-	-	-
2	0,3182	0,1259	0,0188	0,0000	0,0000	-	-	-
3	0,2092	0,2159	0,0597	0,0004	0,0000	-	-	-
4	0,0841	0,2439	0,1268	0,0021	0,0000	-	-	-
5	0,0215	0,1920	0,1918	0,0089	0,0000	-	-	-
6	0,0035	0,1091	0,2141	0,0278	0,0000	-	-	-
7	0,0004	0,0456	0,1803	0,0661	0,0000	-	-	-
8	0,0000	0,0142	0,1162	0,1216	0,0000	-	-	-
9	0,0000	0,0033	0,0578	0,1746	0,0000	-	-	-
10	0,0000	0,0006	0,0222	0,1969	0,0006	0,0000	-	-
11	-	0,0000	0,0066	0,1746	0,0033	0,0000	-	-
12	-	0,0000	0,0015	0,1216	0,0142	0,0000	-	-
13	-	0,0000	0,0003	0,0661	0,0456	0,0004	-	-
14	-	0,0000	0,0003	0,0278	0,1091	0,0035	-	-
15	-	0,0000	0,0000	0,0089	0,1920	0,0215	0,0002	-
16	-	0,0000	0,0000	0,0021	0,2439	0,0841	0,0051	-
17	-	0,0000	0,0000	0,0004	0,2159	0,2092	0,0478	-
18	-	0,0000	0,0000	0,0000	0,1259	0,3182	0,2073	-
19	-	0,0000	0,0000	0,0000	0,0433	0,2679	0,4201	0,2
20	-	0,0000	0,0000	0,0000	0,0066	0,0951	0,3193	0,8

n = 25

x	M
x	10	20	30	50	80	90	95	99
0	0,0479	0,0015	0,0000	0,0000	-	-	-	-
1	0,1814	0,0134	0,0004	0,0000	-	-	-	-
2	0,292	0,0535	0,0032	0,0000	-	-	-	-
3	0,2637	0,1273	0,0144	0,0000	-	-	-	-
4	0,1471	0,2018	0,0436	0,0000		-	-	-
5	0,0530	0,2260	0,0951	0,0004	0,0000	-	-	-
6	0,0124	0,1852	0,1554	0,0020	0,0000	-	-	-
7	0,0019	0,1135	0,1947	0,0074	0,0000	-	-	-
8	0,0001	0,0527	0,1901	0,0218	0,0000	-	-	-
9	0,0000	0,0187	0,1463	0,0509	0,0000	-	-	-
10	0,0000	0,0051	0,0894	0,0953	0,0000	-	-	-
11	-	0,0010	0,0435	0,1444	0,0000	-	-	-
12	-	0,0002	0,0169	0,1776	0,0000	-	-	-
13	-	0,0000	0,0053	0,1776	0,0002	-	-	-
14	-	0,0000	0,0013	0,1444	0,0010	-	-	-
15	-	0,0000	0,0003	0,0953	0,0051	0,0000	-	-
16	-	0,0000	0,0000	0,0509	0,0187	0,0000	-	-
17	-	0,0000	0,0000	0,0218	0,0527	0,0002	-	-
18	-	0,0000	0,0000	0,0074	0,1135	0,0019	-	-
19	-	0,0000	0,0000	0,0020	0,1852	0,0124	-	-
20	-	0,0000	0,0000	0,0004	0,2260	0,0530	0,0007	-
21	-	-	0,0000	0,0000	0,2018	0,1471	0,0126	-
22	-	-	0,0000	0,0000	0,1273	0,2637	0,0848	-
23	-	-	0,0000	0,0000	0,0535	0,2924	0,2691	-
24	-	-	0,0000	0,0000	0,0134	0,1814	0,4036	0,25
25	-	-	0,0000	0,0000	0,0015	0,0479	0,2292	0,75

Voorbeelden

1. De kans op 4 successen in een steekproef van 5 als 80 van de 100 in de populatie een succes zijn is P(X = 4) = 0,4201.

2. Bij een populatie van 100 met 50% successen is de kans op ten minste 8 successen in een steekproef van 10: P(X ≥ 8) = P(X = 8)+ P(X = 9)+ P(X =10) = 0,0380 + 0,0072 + 0,0000 = 0,0452.

3. Bij een steekproef van 20 zitten uit een populatie waarbij 95 van de 100 successen zijn is de kans op X successen gelijk aan 0,2073, Hieruit volgt dat X = 18.